
Binary Tree In Data Structure In Hindi – हेल्लो Engineers कैसे हो , उम्मीद है आप ठीक होगे और पढाई तो चंगा होगा आज जो शेयर करने वाले वो Data Structure के बारे में हैं, तो यदि आप जानना चाहते हैं की Binary Tree In Data Structure In Hindi के बारे में तो आप इस पोस्ट को पूरा पढ़ सकते हैं , और अगर समझ आ जाये तो अपने दोस्तों से शेयर कर सकते हैं।
Binary Tree In Data Structure In Hindi

Tree In Data Structure In Hindi
“ट्री” Tree is a non-linear Data Structure.
- Tree में items sorted क्रम में arrange रहते हैं, tree का use hierarchical type display करने किया जाता हैं अर्थात जिसमे बहुत अधिक data items होते हैं उन्हें प्रदर्शित करने के लिए use किया जाता हैं।
- इसमें सबसे पहला Node Root Node कहलाता हैं और उस node के दो sub-tree होते हैं जिन्हे Normally Right sub-tree और Left Sub-tree कहा जाता हैं।
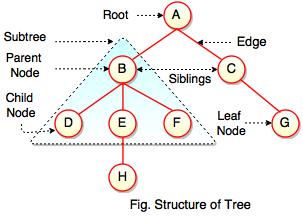
- Data – यह वह data होता है जो node द्वारा store किया जाता है।
- Left Node Pointer – यह node के left child को point करता है।
- Right Node Pointer – यह node के right child को point करता है।
Binary Tree In Data Structure In Hindi
- बाइनरी tree एक ऐसा tree हैं जिसमे केवल दो child हो सकते हैं।
- binary tree empty भी हो सकता हैं या उस tree में 1 भी node हो सकता हैं।
- बाइनरी tree में सबसे पहले node root node कहलाता हैं।
- Root node के दो और node होते हैं जो generally left sub-tree और right sub-tree होती हैं।
- Left sub-tree और Right sub-tree भी empty हो सकती हैं।
- जब tree में एक भी node नही होता है उसे हम empty tree कहते है।
Types Of Binary Tree In Hindi
binary tree निम्नलिखित प्रकार के होते हैं-
- Full binary tree
- Complete binary tree
- Skewed binary tree
- Extended Binary Tree
1. Full Binary Tree In Hindi
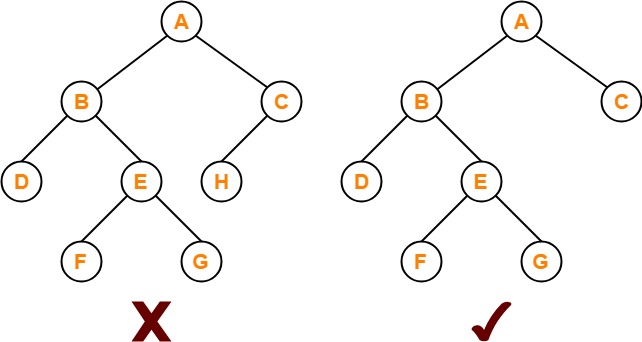
- Full Binary Tree में सभी nodes की या तो 0 या 2 child nodes होती है। आसान शब्दों में कहते तो जिस binary tree की सभी node के या तो left और right दोनों child हो या कोई child ना हो तो ऐसा binary tree full binary tree कहलाता है। Full Binary tree को Strictly binary tree भी कहा जाता है।
- Full Binary Tree में कोई भी node खाली नहीं होता हैं, अर्थात सिंगल node नहीं हो सकता हैं यदि left side वाला node रहेगा तो Right side node भी होगा, अगर सिर्फ एक side node होगा तो वह full binary tree नहीं होगा।
2. Complete binary tree In Hindi
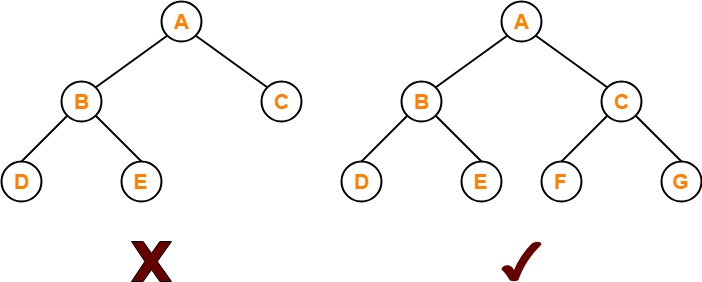
- Complete binary tree में सभी nodes की 2 child nodes हो और जिसकी सभी leaf nodes same level पर हो complete binary tree कहलाता है।
- Complete Binary Tree में left side tree अगर 2 चाइल्ड हैं तो right side के भी 2 child होना जरुरी हैं, अर्थात leaf nodes same level पे होने चाहिए, अगर same level नहीं होगा तो वह Complete Binary Tree नहीं होगा
3. Skewed Binary Tree In Hindi
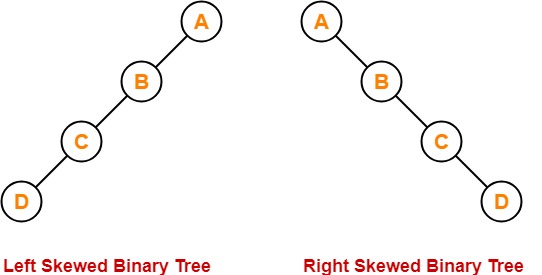
- Skewed Binary Tree में सभी nodes के या तो left या right child nodes होती है, skewed binary tree कहलाता है।
- Skewed Binary Tree में left side child के केवल left side node होते हैं और right side child के केवल right-side node होते हैं।
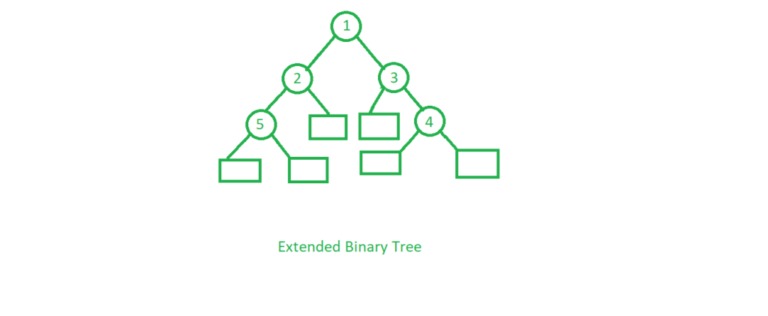
4. Extended Binary Tree In Hindi
- एक binary tree extended binary tree तब कहलाता है जब उसकी सभी nodes के या तो 0 या 2 child nodes हो। Extended binary tree में internal nodes को circle द्वारा और external nodes को rectangle द्वारा दर्शाया जाता है।
- जिन nodes की 2 child nodes होती है वे internal nodes कहलाती है और जिन nodes की 0 child nodes होती है वे external nodes कहलाती है।
Binary Tree Traversal In Hindi
Tree Traversal का अर्थ हैं हर एक Node को visit करना।
एक binary tree को traverse करते समय उसकी हर node को सिर्फ एक बार access किया जाता है और उसके साथ कुछ operation perform किया जाता है।
एक binary tree को 3 प्रकार से traverse किया जा सकता है:-
- In-order Traversal
- Pre-order Traversal
- Post-order Traversal
1. In-order Traversal In Hindi
In-order Traversal में सबसे पहले Left sub-tree को एक्सेस किया जाता हैं और उसके बाद Root Node को access किया जाता हैं last में Right Sub-tree access / Visit किया जाता हैं ।
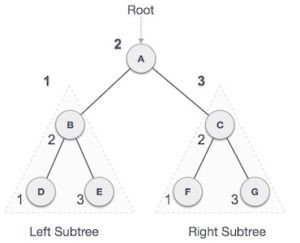
Output:- D → B → E → A → F → C → G
- सबसे पहले हम Left Subtree को access करेंगे तो left side में D हैं और फिर D के left में कोई भी child नहीं हैं, तो अब हम Root Node को access करेंगे तो Root Node B हैं उसके बाद हम Right Subtree अर्थात E को एक्सेस करेंगे, यहाँ B हमारा Root Node की तरह वर्क किया हैं।
- अब हम A को root node मानते हैं तो हमारा left side का subtree access हो गया अब हम root node A को access करेंगे उसके बाद Right side के subtree को access करेंगे।
- Right side में भी एक Root Node C हैं तो उस root node का पहले left subtree visit करेंगे उसके बाद Root Node उसके बाद right subtree access करेंगे।
- तो Root Node C का Left Subtree F को access करेंगे उसके बाद Root Node C को access करेंगे फिर Right Subtree G को access करेंगे।
Algorithm Of In-order Traversal-
INORDERTRAVERSAL ( TREE)-
1. if ( true != Null)
2. Recursively traverse Left Subtree
3. Visit Root Node
4. Recursively traverse Right Subtree
5. Stop
2. Pre-order Traversal In Hindi
Pre-order Traversal में सबसे पहले Root Node को visit किया जाता हैं उसके बाद left subtree को access किया जाता हैं उसके बाद right subtree को access किया जाता हैं ।
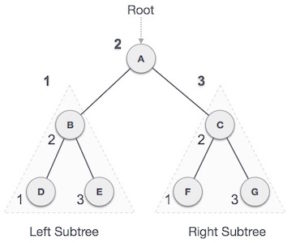
Output – A → B → D → E → C → F → G
- सबसे पहले Root Node A को access करेंगे उसके बाद left sub-tree को access करेंगे।
- लेफ्ट sub-tree में भी B Root Node की तरह काम कर रहा हैं तो हम यहाँ भी पहले B को access करेंगे उसके बाद B के Left Sub-tree को एक्सेस करेंगे।
- B का left sub-tree D हैं उसको एक्सेस करेंगे उसके बाद Right Sub-tree E को access करेंगे
- अब यहाँ A Root node के left sub-tree एक्सेस हो गए हैं अब हम Right sub-tree को access करेंगे।
- Right, sub-tree में भी C एक root node की तरह वर्क कर रहा हैं तो हम पहले Root Node को access करेंगे अर्थात C को access करेंगे उसके बाद Left Sub-tree F को access करेंगे उसके बाद Right Subtree G को access करेंगे।
Algorithm Of Pre-order Traversal-
PREORDERTRAVERSAL ( TREE )-
1. If ( Tree != null)
2. visit Root Node
3. Recursively Traverse Left subtree
4. Recursively Traverse Right subtree
5. Stop
3. Post-order Traversal In Hindi
Post-order Traversal में सबसे पहले Left subtree को access किया जाता हैं उसके बाद right subtree को एक्सेस किया जाता हैं उसके बाद सबसे लास्ट में रुट Node को access किया जाता हैं।
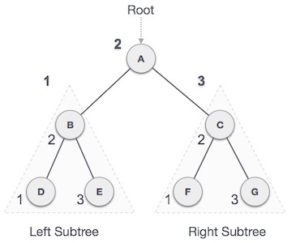
Output- D → E → B → F → G → C → A
- सबसे पहले left subtree को access किया जाता हैं तो यहाँ left subtree D हैं अर्थात सबसे पहले D को access किया जायेगा।
- उसके बाद Right subtree E को access किया जायेगा उसके बाद Root Node B को access किया जायेगा।
- अब हम left side के subtree को access कर लिए अब हम Right side के subtree को access करेंगे।
- Right side में भी एक Root Node C हैं तो उसके left में F को access करेंगे उसके बाद Right साइड के G को access करेंगे उसके बाद रुट node C को access करेंगे।
- उसके बाद सबसे शुरू के Root Node A को एक्सेस करेंगे।
Algorithm Of Post-order Traversal-
POSTORDERTRAVERSAL (TREE )-
1. If ( Tree != null)
2. Recursively Traverse Left Sub Tree
3. Recursively Traverse Right Sub Tree
4. Visit Root Node
5. Stop
Searching A Node In Binary Tree
Binary search tree में किसी node को search करना नयी node को insert करने जैसा ही है। Search की जाने वाली node की value को हर node से compare किया जाता है। यदि वह Value छोटी होती है तो node के left subtree में उसे search किया जाता है नहीं तो right subtree में उसे search किया जाता है।
Inserting A Node In Binary Tree
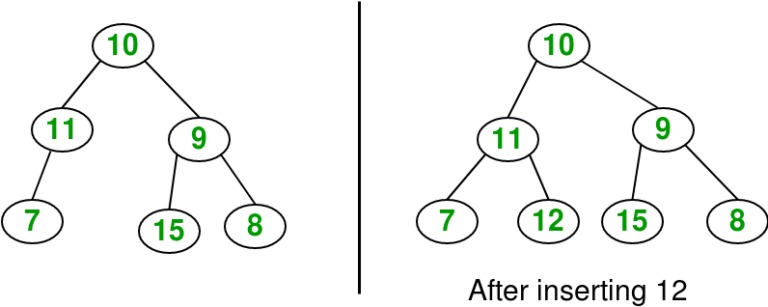
जब आप binary search tree में कोई नयी node insert करते है तो वह operation insertion कहलाता है।
- Insertion के लिए सबसे पहले नयी node को root node से compare किया जाता है।
- यदि नयी node की value कम है तो उसे left subtree में insert किया जायेगा।
- यदि नयी node की value ज्यादा है तो उसको root node के right subtree में insert किया जायेगा।
इसी प्रकार हर node से नयी node को compare किया जायेगा जब तक की नयी node को उसकी सही position नहीं मिल जाये।
Deleting A Node In Binary Tree
Binary search tree में deletion एक complex operation है। क्योंकि binary search tree में सभी nodes आपस में connected होती है। इसलिए किसी भी node को delete करने से दूसरी nodes affect हो सकती है।
इसलिए binary search tree में deletion के 3 अलग अलग case होते है।
- एक leaf node को delete करना।
- एक ऐसी node को delete करना
- जिसके सिर्फ एक ही child node हो।
- एक ऐसी node को delete करना जिसके 2 child nodes हो।

Conclusion Binary Tree In Data Structure In Hindi
दोस्तों इस पोस्ट को पूरा पढने के बाद आप तो ये समझ गये होंगे की Binary Tree In Data Structure In Hindi और आपको जरुर पसंद आई होगी , मैं हमेशा यही कोशिश करता हु की आपको सरल भाषा में समझा सकू , शायद आप इसे समझ गये होंगे इस पोस्ट में मैंने सभी Topics को Cover किया हूँ ताकि आपको किसी और पोस्ट को पढने की जरूरत ना हो , यदि इस पोस्ट से आपकी हेल्प हुई होगी तो अपने दोस्तों से शेयर कर सकते हैं।